How do we add and subtract rational expressions?

So what is a rational expression?
A rational expression is an expression that is the ratio of two polynomials.
So what does that even mean? Well basically it's a fraction with polynomials.
Hers's an example: 
                              
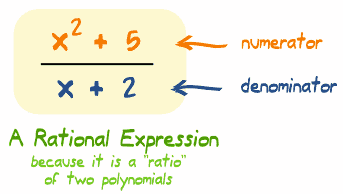
Okay so now that you know how a rational expression looks like, what happens when you add two rational expressions? 
Well, let's say you have to add (x-5)/(x^2-9) + (x+12)/(x+3), how can you add them? If you had to add 2/5 + 1/5 you would get 3/5 but that's because their denominators is the same, but for our little rational expression above, the denominators are different so what do we do?!?!
Well we actually already mentioned the answer, we must find the Least Common Denominator! 
(But before we go any further, let's look at a picture so we can see the problem with our eyeballs and possibly better understand it!)
                        
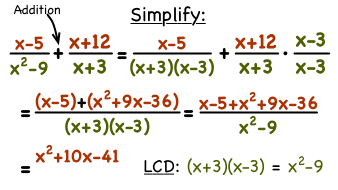
So the first step to solve this problem would be to factor out the denominator: (x^2-9) which would become (x-3)(x+3) and if we look at the other denominator it already has a denominator of (x+3) which means that all you have to do to make it equal with the other denominator is multiply it by (x-3). Don't forget that if you multiply that rational expression by (x-3) you must multiply BOTH the numerator and denominator!
Once you do that you should end with (x+5) + (x^2+9x-36) all over (x+3)(x-3) and your final answer should be (x^2+10x-41)/(x^2-9).