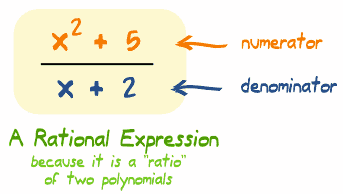Why is the name Pythagorean Identity appropriate?

When you think of Pythagorean Identity, the first thing that pops into your head is probably the Pythagorean Theorem. If so, then that's great! This is exactly where the term Pythagorean Identity came from!

 Now that we have a triangle with  a hypotenuse of 1, we can use the Pythagorean theorem to derive the special trigonometry functions that we will use to form the Pythagorean Identity.

So here's our formula: a^2+b^2=c^2
(for our purposes, a will be x and b will be y)
Now let's find the trig functions. We know the following:
Sin()= opposite / hypotenuse = y / 1 = y
Cos()= adjacent / hypotenuse = x / 1 = x

By substituting this into our triangle, our result will be the following:

And now that we have our trigonometry functions, all we have to do is plug them in to the Pythagorean Theorem! 

Which would look like the following: 

a^2+b^2=c^2  (remember for our purposes, for our previous triangle: a=x and b=y) 

cos^2+sin^2=1 --> which is the first Pythagorean Identity!

So I hope you now understand how the Pythagorean Identity got its name, because of the Pythagorean Theorem! 

How do we use inverse variation?

So how does an inverse variation problem look like?
Like this -->                              

x	y
3	20
6	10
12	y

Well call this problem an inverse variation relationship. We say that the X value varies inversely with the Y value. In simpler words, as the X value goes up, the Y value goes down and vise-versa. 

In order to solve this problem, you can use the following equation:  

REMEMBER: An inverse variation will always have a constant value --> K.

K will be the product of the X and Y values.

So for our little equation: 3*20=60 and 6*10=60, so our constant (k) must be 60.

Now let's plug in all the values:  y=60

                                     12

So the missing Y value must be 5! 

Yay, we are finished with this problem. It's really simple!

How do we simplify complex fractions?

I remember how many students disliked math because of the fractions, they thought fractions were just plain ugly. And it's true, that fractions might complicate a problem but it is not impossible!
Now, let's take things a step furhter and solve complex fractions. What are complex fractions? How do they look like? Here is an example:

                                                
Okay, it looks pretty tough but we're tougher! And we can get through this problem.
The way we're going to set out to solve this problem is by finding common denominators for both fractions.
For the first fraction on top, you will have to multiply 4 by x in the numinator and denominator. Your total answer for the top should be 4x+1 over x.
Then for the bottom fraction you should multiply the 3 by x^2 in the numinator and denominator. Your total answer for the bottom should be 3x^2+2 over x^2.
Then all you have to do after that is keep change flip, which means you have to keep the top fraction, change it from a division problem into a multiplication problem, and flip the bottom fraction.
Once you do that, you will be able to cancel out an x, and your final answer should be: 4x^2+x over 3x^2+2.

I know there are some of you that are visible learners so just for you guys (and for everyone else too) here is the problem:

                             

How do we solve quadratic equations by completing the square?

Okay, so first let's review quadratic equations and how to solve them.

How does a quadratic equation look like? And how do you solve them? 

Well a quadratic equation is an equation that has an exponent of two inside the equation. And in order to solve it, you have to plug it in into the following formula:

                             

So let's say you have the following equation: 3x^2+6x-7=0 All you have to do is plug in a,b, and c into the quadratic formula to find x. REMEMBER THAT YOU WILL ALWAYS GET TWO ANSWERS FOR A QUADRATIC EQUATION!  

Now that you know how to solve a quadratic equation, here's a little story for you to read:

      

Okay, now let's take it a step further and instead of just plugging the equation into the formula, what if you're asked to complete the square? :o

No worries, it's quite easy. 

First let's take an equation.

Here you go --> 2x^2+8x=10

Divide the whole equation by 2 to get x^2+4x=5 

Then you have to divide the bx term by two to get 2 and then square it to get 4. This will now be your c term and you will have to add this to the other side. You will end up with x^2+4x+4=9. You have completed the square! :D

So just to sum it all up, here are the steps you should follow for any problem in which you have to solve a quadratic equation by completing the square:

Step 1: Put the variable terms on one side of the equation and the constants on the other side. Make sure the coefficient of the squared term (a) is 1.

Step 2: Find the value that will complete the square by taking half of the linear term coefficient (b) and squaring it. 

Step 3: Add the value to each side.

Step 4: Factor the perfect square.

Step 5: Solve by taking the square root of both sides. 

Imaginary numbers

Did you know that there is such a thing as imaginary numbers? Well f you didn't know, then now you do!

So how does an imaginary number look like? Can you even see it? Since it's imaginary and all...

As it turns out, you can see them, and here's an imaginary number --> i

So when do we use imaginary numbers? Well have you ever come across an equation where you got No Solution? Or more specifically, No Real Solutions? 

An example of such a situation is when you try to find the square root of a negative number. 

The thing with square roots is that you cannot find the square root of a negative number, and this is where imaginary numbers come into place! So let's look at the following chart to see how to read imaginary numbers.

i=√-1

i^2=-1

i^3=-i

i^4=1

And now let's say you have √-9 so would that be an imaginary number? Why yes it would, but you may ask, "It doesn't look like an imaginary number because it doesn't have the little i thingy." That is true, so let's find out how to convert a negative radical number into an imaginary number with an i. 

So the first step to do this would be to take out the negative number, like this --> 

√9 √-1 Then √9 would turn into 3 and √-1 would turn into i.  And the last step is to combine them together, and your final answer should be 3i!

                     

                       Poor imaginary numbers, don't forget about them :(

How do we perform composition of functions?

Okay well we are all aware of what functions are, right? This is a function --> f(x)=3x+5

That seems easy enough to solve, just plug in a number for x to find f(x). 

Now, here's another function --> g(x)=x+6

It still doesn't look so bad, it's just like the same one, plug in a number for x to find g(x). 

But what if you are asked to find f(g(3))?? :O

                      

                                                WOAH! How do you solve that?

                                                 

Well let's take it step by step and break it down.

First we will need to find out how the equation will look like.

We know that f(x)=3x+5 and g(x)=x+6, so how would f(g(3)) look like?

Well lets start inside the parenthesis --> g(3)=(3)+6 so g(3)=9!

And now we plug the answer of g(3) inside the function f(x) which should be f(9)=3(9)+5. and f(9)=32.

So just remember, whenever you have a composite function just take a deep breath and break it down into steps.

1. Write out what you know, the functions.

2. Start with the inner function, solve it.

3. Replace the x in the outer function with the answer you got from the inner function. 

4. Solve the function.

5. Smile and congratulate yourself on a job well done! :D

How do we find excluded values?

Let's say we have an expression that looks something like this -->      -7   
                                                                                                        x-5
Usually we have to find when the value x would satisfy the expression but what about when we have to find the excluded values, what do we do?
Well usually when we have to find the excluded values, the expression will be either in fraction form or in a radical form --> √x-5

There are two rules for finding the excluded values:
1. The denominator CAN'T be ZERO!!
2. Radical can't be negative. 
So first, let's solve the fractional expression!
  -7       First let's take the denominator and make it not equal to zero.
x-5
x-5=0 And then all you have to do is add 5 to both sides.
Your answer should be x=5 so the excluded value is 5!

Now let's take a look at that radical expression! √x-5
We know that the radical cannot be a negative number so in order to find the excluded values we must take out the expression inside the radical and make it less than 0.   x-5<0 
Then you just add five to both sides.
Your final answer should be x<5

How do we recognize functions?

A Relation is a set of ordered pairs. The set of ordered pairs in a relation can be shown using braces, tables, graphs, and mappings. 

A Function is a relation that assigns exactly one output value (range/y-value) for each input value (domain/x-value).

Recognize functions by making sure the same input value (x) is NEVER repeated. 

Some characteristics of a function are:
1. Each x-value must be matched with a y-value
2. Some y-values may not be matched with a x-value
3. Two or more x-values may be matched with the same y-value
4. A x-value CANNOT be matched with 2 different y-values.

How do we add and subtract rational expressions?

So what is a rational expression?
A rational expression is an expression that is the ratio of two polynomials.
So what does that even mean? Well basically it's a fraction with polynomials.
Hers's an example: 
                              
Okay so now that you know how a rational expression looks like, what happens when you add two rational expressions? 
Well, let's say you have to add (x-5)/(x^2-9) + (x+12)/(x+3), how can you add them? If you had to add 2/5 + 1/5 you would get 3/5 but that's because their denominators is the same, but for our little rational expression above, the denominators are different so what do we do?!?!
Well we actually already mentioned the answer, we must find the Least Common Denominator! 
(But before we go any further, let's look at a picture so we can see the problem with our eyeballs and possibly better understand it!)
                        
So the first step to solve this problem would be to factor out the denominator: (x^2-9) which would become (x-3)(x+3) and if we look at the other denominator it already has a denominator of (x+3) which means that all you have to do to make it equal with the other denominator is multiply it by (x-3). Don't forget that if you multiply that rational expression by (x-3) you must multiply BOTH the numerator and denominator!
Once you do that you should end with (x+5) + (x^2+9x-36) all over (x+3)(x-3) and your final answer should be (x^2+10x-41)/(x^2-9).